Overview

The goal of this blog is to go over some important concepts in statistics and probability theory that should be well understood to get a stronger grasp on machine learning. This blog post assumes the following prequisite knowledge:

1. A strong grasp on math notation
2. Basic probability theory (eg. Kolmogorov axioms, CDF, PDF)
3. Basic linear algebra (eg. vectors, matrices, vector spaces, bases, coordinates, and eigenvalues/vectors)
4. Being able to read NumPy code.

I will begin with crucial basics and work up to some other important concepts.This post combines theory and code; you learn the concept using math and see it in action using code.

The basics

Expected value

For a random variable $X$, the expected value of $X$, denoted $\mathbb{E}[X]$ is the value you would expect if you averaged over an infinite number of trials. The way in which this is computed depends on whether $X$ is a discrete or a continuous random variable.

Discrete case

When $X$ is a random variable with a finite list of possible outcomes, $x_1, x_2, \dots, x_N$, then

This can be seen as a weighted sum of values, where the weight for $x_i$ is $P(X=x_i)$, so values that are more likely will contribute to the sum.

Example

Let $X = 0$ denote a coinflip of heads, and $X = 1$ denote tails, where $P(X = 0) = P(X = 1) = 1/2$, then our expected value should be directly in the middle of zero and one, since each outcome has the same probability (or weight); indeed, when we plug this into the equation above, we see that

Now, what if instead we had a biased coin? That is, what if one outcome was much more likely than the other? For example, let’s set $P(X = 0) = 0.1$ and $P(X = 1) = 0.9$. In this case, our expected value should be much closer to 1 than 0, since tails is a lot more likely. Once again, we see that the the output of the equation matches our intuition:

Continuous case

The notion of likelihood

In the continuous case, we have an infinite number of possible outcomes, which means that $P(X=x) = 0$ for all possible $x$. To build intuition, consider a proof by contradiction. Suppose there exists some nonzero probability $\epsilon_x > 0$ assigned to each individual outcome $x$. Then, summing over an infinite number of such outcomes would yield an infinite total probability:

which contradicts the requirement that the total probability over the sample space must equal 1. Therefore, the only consistent assignment is that each individual outcome has probability 0.

You might be thinking “Ok, I understand why probabilities are zero, but surely there are some events that are more likely than others”. This is indeed true. For example, in theory, height is a continuous random variable; there are certainly some heights that are more common than others. This idea is captured through the notion of likelihood. For each possible value of $x$, we can assign a value $p(x) \geq 0$ which represents how likely we are to observe $x$ (it is very important to keep in mind that it’s not actually the probability of $x$). We add the additional restriction that $\int_{-\infty}^{+\infty}p(x)dx = 1$ (so the area under the likelihood curve is 1).

Coming up with an equation for expected value

Recall that earlier our expected value was computed as a weighted sum of values, where the weights are point probabilities. In the continuous case, we have seen that probabilities are swapped out for likelihoods, and since we have an infinite number of values, we should take an integral. Thus, our expected value can be written as

Again, the idea here is that the points with higher likelihood have a greater weight in the computing the expected value.

Example

Important Note

A concept that is often glossed over is that in practice we typically don’t compute the actual expected value, since that would require knowing the true underlying distribution of our data (which is often unrealistic). Instead, we estimate it using an unbiased estimator. This is a value that we can compute using our dataset that estimates the true value of some parameter; as the amount of data increases, we approach the true value. More formally, an estimator $\hat{\theta}$ is said to be unbiased for parameter $\theta$ if $\mathbb{E}[\hat{\theta}] = \theta$. For example, suppose we are trying to estimate $\mu_X = \mathbb{E}[X]$; it can be shown that the sample mean $\bar{X} = \frac{1}{N} \sum_{i=1}^N x^{(i)}$ is an unbiased estimator of $\mu_X$ (so $\mathbb{E}[\bar{X}] = \mu_X$). As we will see later, unbiased estimators also exist for many other parameters (such as the variance and covariance). We will also show later that these unbiased estimators indeed converge to the parameters they are trying to estimate.

For the continuous case, showing a worked out example is a bit trickier. Instead, we will take some real world data and estimate the expected value using an unbiased estimator. An unbiased estimator for the expected value is the sample mean (typically denoted $\bar{X}$):

Again, remember that this is not actually the expected value. This is a value we can compute to estimate the expected value.

For our real world data, I downloaded height and weight data from Kaggle. For now, we will focus on only the height data.

First, it would be nice to plot the probabilities of each height; the problem is that heights are a continous variable, so the probability of an exact height is very low (eg. the odds that someone has a height of 66.72 inches is quite low, but the probability of a height close to 66.72 might be quite high). To deal with this, we will group our data points into bins. These are simply intervals in the data; thus, instead of counting the probability of an exact value, we will compute the probability that a point falls into a bin. Here is a visualization of our data being split into $n=30$ bins, where the boundaries of the bins are marked by red-dotted lines:

Using the same bins, we can plot the density of our data (where density for a bin is ( of points in bin) / (total of points)):

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


df = pd.read_csv("./heights/SOCR-HeightWeight.csv")
heights = df["Height(Inches)"].to_numpy()
n_bins = 30
bin_centers, probabilities = split_bins_and_probabilities(heights, n_bins)

 Plot the histogram
plt.hist(heights, bins=30, density=True, alpha=0.5)
plt.xlabel('Height')
plt.ylabel('Density')
plt.title(f"Height densities with n={n_bins} bins")
plt.show()

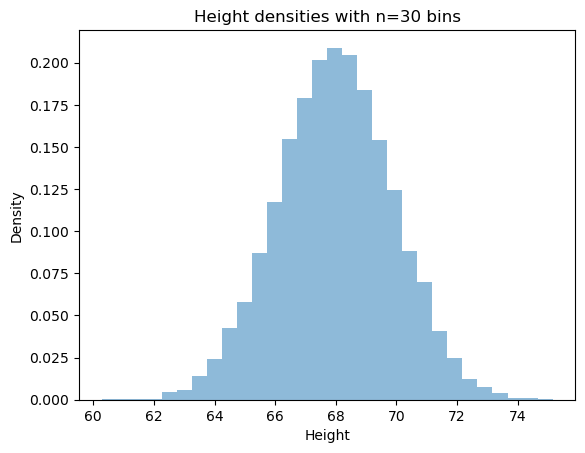
Now that the concept of bins is (hopefully) clear, the plot should hopefully make sense. Now we can simply compute the expected value. As seen above, we can simply do this by calculating the mean

def E(X):
    return np.mean(X)

E(heights)  returns 67.99

Using this, let’s plot our data again, this time including the mean:

E_height = E(heights)

plt.hist(heights, density=True, bins=n_bins, alpha=0.5)
plt.axvline(x=E_height, color='red', linestyle='--', linewidth=2, label=f'Expected value: {E_height:.2f}')

plt.legend()
plt.xlabel('Height')
plt.ylabel('Density')
plt.title('Distribution of Heights')

plt.show()

In this case, our expected value is roughly $68$, which seems to be roughly at the peak of our data. Importantly, note that the expected value will not always be at the peak of the data; the reason it’s in at the peak in this case is because the data is symmetrical around the peak.

Expected Value of the Function of a Random Variable

When reading machine learning material, you will see expected value come up a lot, but in many cases the notation will look much more complex; for example, $\mathbb{E}[\mathbb{H}(X)] = \int_{\infty}^{\infty} p(x)\mathbb{H}(x)dx$. Do not let this scare you. This is the expected value of a function of a random variable. The concepts here are identical to before: we want to know the value if we average over an infinite number of trials. The only difference here is that before we were looking at the expected value of $X$, and now we’re looking at the expected value of some function of $X$. So to find the average of $\mathbb{H}(x)$ over an infinite number of trials, we multiply $\mathbb{H}(x)$ by the likelihood of the input, $p(x)$.

Example

Let’s dig a bit deeper by looking at the example from above. We will take the height of each person and double it. That is, we will apply the function $f(x) = 2x$ to each height in our dataset, and we will compute the new expected value. Before doing this, can you guess what it will be?

def f(x):
    return 2*x

E_f = E(f(heights))

plt.hist(f(heights), density=True, bins=30, alpha=0.5)
plt.axvline(x=E_f, color='red', linestyle='--', linewidth=2, label=f'Expected value: {E_f:.2f}')

plt.legend()
plt.xlabel('Double Height')
plt.ylabel('Density')
plt.title('Distribution of f(x) = 2x')

plt.show()

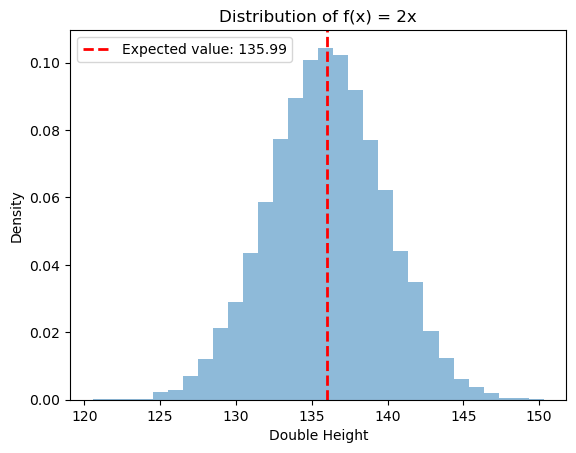
The new expected value $\mathbb{E}[f(X)] = \mathbb{E}[2X]$ is twice the mean from before! This makes sense, since each input of $f$ maps to a unique output, the distribution should remain the same, but with each value doubled (ie. if $x_i$ has likelihood $p_i$ in our original data, then $f(x_i)$ will have the same likelihood in the our new data).

Key Takeaways on Expected Value

1. Expected value tells you the value you would expect is you averaged over the outcome of an infinite number of trials. In other words, it’s a theoretical mean of the data (as such, the terms mean and expected value are often interchangeable).
2. You can take the expected value of functions of random variables.
3. You can estimate the expected value using the sample mean $\bar{X}$.

Variance

For a variable random variable $X$, the variance of $X$ is $\text{Var}(X) = \sigma^2_X = \mathbb{E}[(x - \mathbb{E}[X])^2)]$. This can be read as the average squared difference from the mean. Note this is squared, meaning the variance must be positive. Intuitively, this measures the spread of the data, or how much it varies from the mean. To make this slightly more readable, we will denote the expected value of $X$ as $\mathbb{E}[X] = \mu_X$; this is common notation. Notice that the variance is the expected value of function of a random variable. In this case, it’s the function $f(X) = (X - \mu_X)^2$ (where we used our new notation for the mean). Thus, all the same ideas from above still apply; namely, that the way in which this is computed will depend on whether $X$ is a dicrete or a continuous random variable.

In the discrete case:

In the continuous case:

Example

Let’s look at this in action by jumping back into our example of height data. Again, we will be using an unbiased estimator for the variance. In this case, the unbiased estimator for the variance is the sample variance, often denoted $S^2$:

note that the reason we divide by $n-1$ is not immediately obvious and is beyond the scope of this blog.

We can now start our investigation by writing a function that computes the sample variance. Again, this is pretty straightforward.

def V(X):
    mu = E(X)
    squared_diffs = np.sum((X - E(X))**2)
    s_2 = squared_diffs / (len(X) - 1)
    return s_2

V(heights)  3.62

Again, it’s important to note that variance gives us the average squared difference from the mean. To get the non-squared difference you can take the square root of the variance, $\sqrt{Var(X)} = \sqrt{\sigma_X^2} = \sigma_X$; this value is so frequently used that it has a name: the standard deviation. Let’s visualize our data with the variance to see the regions that are one standard deviation to the left and right of the mean:

 Compute expected value and variance from the raw data
E_height = E(heights)
var_height = V(heights)
std_height = np.sqrt(var_height)
 Plot histogram
plt.hist(heights, density=True, bins=n_bins, alpha=0.5)
 Expected value line
plt.axvline(x=E_height, color='red', linestyle='--', linewidth=2, label=f'Expected value: {E_height:.2f}')
 Variance range lines (±1 std dev)
plt.axvline(x=E_height - std_height, color='blue', linestyle=':', linewidth=2, label=f'-1σ: {E_height - std_height:.2f}')
plt.axvline(x=E_height + std_height, color='blue', linestyle=':', linewidth=2, label=f'+1σ: {E_height + std_height:.2f}')
 Labels and legend
plt.legend()
plt.xlabel('Height')
plt.ylabel('Density')
plt.title('Distribution of Heights with Expected Value and Variance')
plt.show()

If our data were more closely centered around the mean, our variance would be smaller, and if it were more spread out, the variance would be larger.

Key Takeaways on Variance

1. Variance tells you the expected squared distance from the mean.
2. Variance is the expectation of a function of a random variable.
3. Variance can be estimated using sample variance $S^2$.

Higher dimensional data

Expected value in higher dimensions

In machine learning, we often deal with higher-dimensional data. For example, our input data might contain the heights and weights of various individuals. In this case, each data point can be represented as a 2D vector, where the first element is the height and the second is the weight. That is, our dataset is a set of points $x^{(i)} = [x^{(i)}_1, x^{(i)}_2]$, where $x^{(i)}_1$ is the height of individual $i$, and $x^{(i)}_2$ is their weight.

In this case, instead of computing a scalar for the expected value, we compute a vector $\mu_X = [\mu_{x_1}, \mu_{x_2}]$, where $\mu_{x_1}$ is the expected value looking only at height, and $\mu_{x_2}$ is the mean looking only at weight.

Vectorizing our equations

In machine learning, we often deal with high-dimensional data (ie. our data points are usually high-dimensional vectors). In machine learning, we will often vectorize equations to create concise versions of equations that scale to any dimensionality (also, when programming, vectorized equations allow you to avoid loops, often making code faster and easier to read). Accordingly, you should get comfortable with vector notation. In the remainder of this blog I will first introduce equations in their “scalar form” and then re-write in their vector notation. It might be helpful to first look at scalar equations, try to figure out the vectorized form, then look to see if you were right.

Let’s start this off with the simplest example: the sample mean, $\bar{X}$.

Recall the equation for the sample mean:

How can we write this in vector form? If our data is a set on $n$ 1D datapoints, $X \in \mathbb{R}^{N \times 1}$, we can compute the sample mean mean as dot product:

where $\mathbb{1} \in \mathbb{R}^{n \times 1}$ is a vector of ones. Now what if we want to generalize this even further? That is, what if our data points aren’t just 1D, but $d$-dimensional? Suppose we have a dataset $X \in \mathbb{R}^{n \times d}$. It turns out we can do the exact same thing! The result is now a $1 \times d$ vector where

In words, the $j$-th component is the mean of the $j$-th feature. In other words, we have computed the mean of each column of our dataset.

def E(X):
    N = len(X)
    mean = (1 / N) * np.ones(N).T @ X
    return mean

Example

Again, let’s understand this via an example. This time, we will need 2D data. Luckily, the data from earlier contains both the heights and weights of individuals. To start, we will simply plot our data to visualize it.

We can easily compute our expected value vector using the equation above:

 Get the data
df = pd.read_csv("./heights/SOCR-HeightWeight.csv")
heights = df["Height(Inches)"].to_numpy()
weights = df["Weight(Pounds)"].to_numpy()
X = np.array([heights, weights]).T

mu_height, mu_weight = E(X)

 Plot raw data
plt.scatter(heights, weights, alpha=0.2, s=10, color="blue", marker="x", label='Raw data')

 Plot mean point
plt.scatter(mu_height, mu_weight, color="red", s=100, label='Mean vector (μ)', marker='o')

 Annotate mean (optional)
plt.annotate(f"μ = ({mu_height:.1f}, {mu_weight:.1f})", 
             (mu_height, mu_weight),
             textcoords="offset points",
             xytext=(10,10), 
             ha='left',
             fontsize=12,
             color="red")

 Labels and legend
plt.xlabel("Height (Inches)")
plt.ylabel("Weight (Pounds)")
plt.legend()
plt.title("Height vs. Weight with Mean Vector")
plt.show()

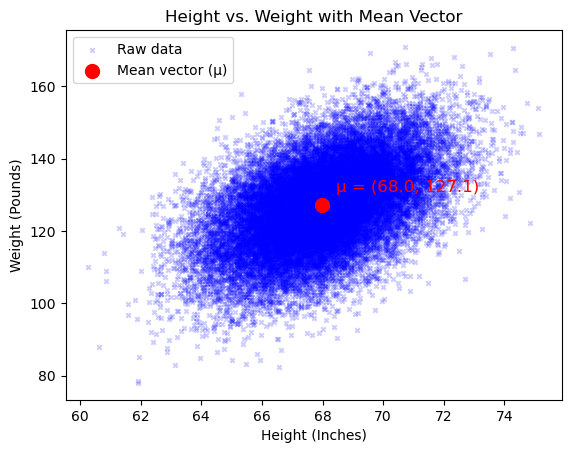
As we saw above, the mean can be generalized to $d$-dimensions. The subsequent section will go over covariance, which is the higherdimensional generalization of variance.

Key Takeaways on Higher Dimensional Data

1. Machine learning uses a lot of high dimensional data
2. We can treat each feature as its own random variable
3. It’s important to understand vecorized equations

Covariance

The covariance between two random variables $X$ and $Y$ is $\text{Cov}(X,Y) = \mathbb{E}[(X - \mu_X)(Y - \mu_Y)]$. This equation takes every possible pair of $X$ and $Y$ and takes the product of their differences from their respective means. Intuitively, if this is:

1. Positive it means that on average, when $X$ is greater than its mean, so is $Y$ (and vice-versa), which means they grow in the same direction.
2. Negative means that on average, when $X$ is above its mean then $Y$ is below (or vice-versa), which means they grow in opposite directions.
3. Close to 0 means neither of the above are true, so it must mean there is no relationship in the direction in which they grow (not the same nor the opposite)

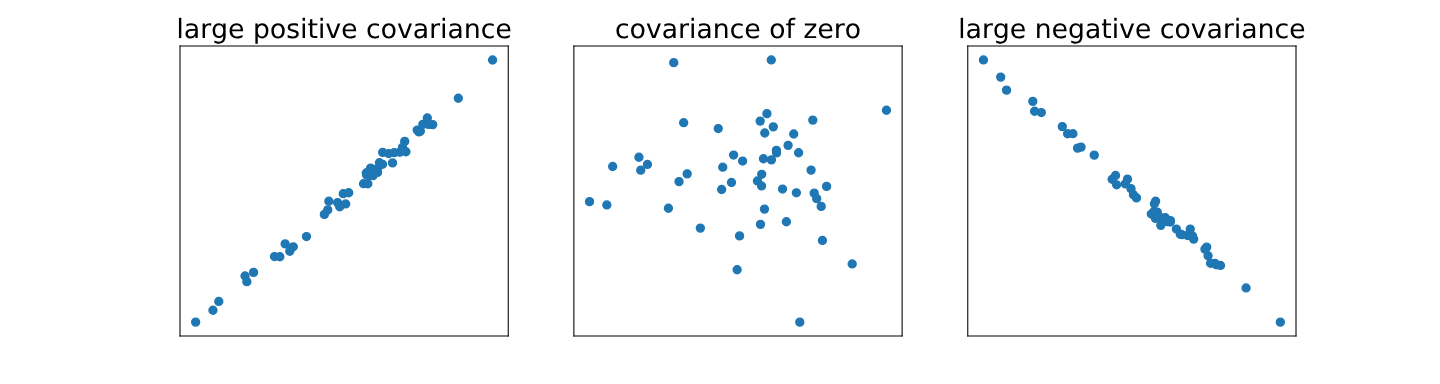
As usual, the way in which this is computed depends on whether we’re in the discrete or continuous case:

In the discrete case:

In the continuous case:

Note that $\text{Cov}(X,X) = \text{Var}(X)$.

When working with higher dimensional data, we are interested in the covariance between all combinations of random variables. This introduces the notion of the covariance matrix, $\Sigma$. Given random variables $X_1, \dots, X_d$ we define $\Sigma \in \mathbb{R}^{d \times d}$ such that

This definition implies that the elements on the main diagonal are of the form $\Sigma_{i,i} = \text{Cov}(X_i, X_i) = \text{Var}(X_i)$. We will do a much deeper dive into the covariance matrix later.

Unbiased estimator and vectorized version

As usual, we will not actually compute the covariance / covariance matiex. Instead, we will use an unbiased estimator. This time it’s the estimator $S_{XY}$:

Again, let’s start with the simplest case and work our way up. So, we will start by seeing how we can vectorize variance (which is just a special case of covariance). If our data is a set of $n$ 1D datapoints, $X \in \mathbb{R}^{N \times 1}$, we can compute the sample variance as a dot product:

Again, it turns out that this exact same formulation generalizes to $d$-dimensional data, where

Using code, we can compute the covariance matrix:

def Cov(X):
    n = X.shape[0]
    mean = E(X)
    diff = (X - mean)
    cov = 1/(n-1) * diff.T @ diff
    return cov

Example

Let’s look at each of the values in the covariance matrix for our height and weight data:

Cov(heights, weights)

array([[  3.61638215,  11.15102917],
       [ 11.15102917, 135.97653199]])

The first element on the diagonal is the variance of the height (which is the exact same value we computed before). The second is the variance of the weight. The values on the outer diagonal are the same, and are the covariance of the height and weight. Notice that it’s positive, which is what we would expect; a positive covariance means that both height and weight grow together (ie. as weight increases height also increases).

Key Takeaways on Covariance

1. Covariance tells you how two random variables grow together
2. Variance is a special case of covariance
3. The covariances for all combinations of random variables in the dataset are represented in the covariance matrix
4. Covariance can be estimated using $S_{XY}$

Correlation

Often when we’re looking at the relationship between two variables we care more about the correlation than the covariance. The idea behind correlation is to normalize our covariance; this is a common term in machine learning. Generally, it means to rescale your data to fit in a particular range. For example, a vector can be normalized into a unit vector, which rescales it to a vector of length one. In this context, we normalize our covariance into the range $[-1,1]$ to obtain our correlation. Correlation is defined as:

where the denominator normalizes the data. The reason why this normalizes the data might not immediately be obvious. To see this, let’s look at the vector form of the unbiased estimator seen above (here $X, Y\in \mathbb{R}^n$ so both are simply vectors):

Thus, this can be seen as the dot product of two unit vectors. This is exactly the cosine of the angle $\theta$ between the two centered data vectors Since $\cos(\theta) \in [-1, 1]$, the correlation is always in that range.

Why is this useful?

Unlike covariance which can be any real number, correlation gives a standardized way to measure how related two variables are. As such, it gives us a way to compare results across different experiments with data of different scales.

Example

Using our dataset, we can compute the correlation of our data:

def corr(X, Y):
    centered_x = X - E(X)
    centered_x_norm = np.linalg.norm(centered_x)
    
    centered_y = Y - E(Y)
    centered_y_norm = np.linalg.norm(centered_y)
    
    corr = (centered_x).T @ centered_y / (centered_x_norm * centered_y_norm)
    return corr

corr(heights, weights)  0.50

We get a correlation of 0.50, which means height are weight are moderately correlated.

Key Takeaways on Correlation

1. Correlation is just normalized covariance
2. Correlation provides a way to compare data from different experiments

The Gaussian

The Gaussian or Normal distribution is an extremely common distribution in machine learning. It’s important to understand where it comes from and how it works.

Univariate Gaussian

In the univariate case, the equation for Gaussian is:

Let’s start by getting some intuition for how and why the parameters $\mu$ and $\sigma$ control the shape of the curve.

Try this Demos link to play around and generate the following plot.

Here is a plot of the quadratic term $-(x-\mu)^2/{2\sigma^2}$ :

Changing $\mu$ will shift the location of the maximum (ie. where the function evaluates to 0). Decreasing $\sigma$ makes the rate at which the function decreases higher (ie. it tightens it up). Here we have set $\sigma$ to 1, 0.5, and 0.1, which correspond to the red, orange, and green lines respectively:

Next, when we pass it through the exponential function, we make all the values positive (since $e^x > 0, \forall x$ ). Since the quadratic has a maximum at 0 when $x=\mu$, our inputs to the quadratic are all $\leq 0$. Also, since the the quadratic gets steeper and steeper as we move away from the mean, the exponential will get flatter and flatter (since the exponential approaches 0). In the following image is the mapping from a quadratic to the exponential $e^{\left(-\frac{1}{2\sigma^{2}}\left(x-\mu\right)^{2}\right)}$ (in purple):

Finally, we divide by the constant $\sqrt{2\pi\sigma^2}$ to ensure that the function integrates to one. The final result is a standard normal distribution, shown in blue:

Advancing to the multivariate case

Now we describe the probabilities over a vector $x \in \mathbb{R}^D$. Now, our distribution is defined by a mean vector $\mu \in \mathbb{R}^D$ and a covariance matrix $\Sigma \in \mathbb{R}^{D \times D}$. The entry $\Sigma_i,j$ is the covariance $\text{Cov}[X_i, X_j] = \mathbb{E}[(X_i - \mu_i)(X_j - \mu_j)]$ We end up with the equation:

In the same way as before, the quadratic term returns a scalar that decreases as $x$ grows further from the mean, the curve becomes bell-shaped as a result of the exponential, and we divide by the first term to ensure that it integrates to one. In the next section, we inspect this further, with the example of the bivariate Gaussian, since this is the easiest to visualize.

Forms of the covariance matrix

There are a few important types of forms the covariance matrix can take:

• Spherical: diagonal matrix where all elements on the diagonal are the same (ie. $\Sigma = \sigma I$)
• Diagonal: diagonal matrix where all elements on the diagonal aren’t necessarily the same
• Full: Non-diagonal

Let’s write some code to generate some of this data. This can be done easily using some functions built into to NumPy. Let’s see what each of these look like:

mean = np.array([0, 0]) # mean of zero

# Covariance matrices
spherical_cov = np.array([[1, 0], [0, 1]])
diagonal_cov = np.array([[5, 0], [0, 3]])
full_cov = np.array([[5, 1], [1, 3]])

n = 1000  # number of samples

# Generate samples
x1, y1 = np.random.multivariate_normal(mean, spherical_cov, n).T
x2, y2 = np.random.multivariate_normal(mean, diagonal_cov, n).T
x3, y3 = np.random.multivariate_normal(mean, full_cov, n).T

# Create side-by-side subplots
fig, axes = plt.subplots(1, 3, figsize=(15, 5), sharex=True, sharey=True)

# Plot each distribution
axes[0].scatter(x1, y1, s=5, color='blue', alpha=0.5)
axes[0].set_title("Spherical Covariance")

axes[1].scatter(x2, y2, s=5, color='green', alpha=0.5)
axes[1].set_title("Diagonal Covariance")

axes[2].scatter(x3, y3, s=5, color='red', alpha=0.5)
axes[2].set_title("Full Covariance")

# Common formatting
for ax in axes:
    ax.set_aspect('equal')
    ax.grid(True)
    ax.set_xlim(-10, 10)
    ax.set_ylim(-10, 10)

plt.tight_layout()
plt.show()

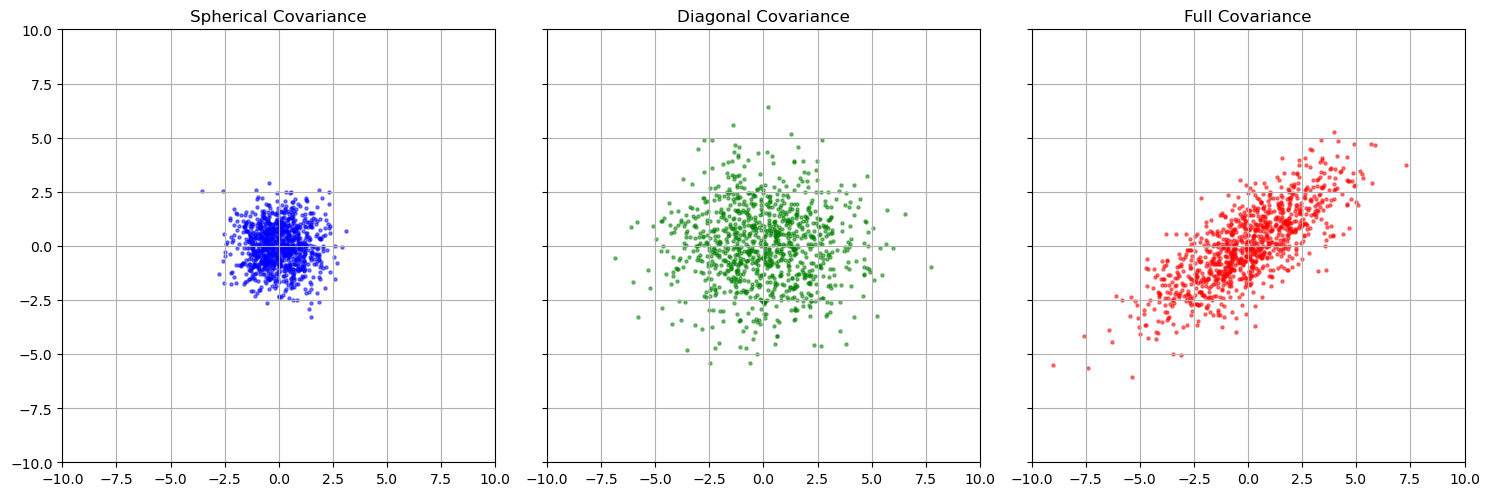
We can see that a diagonal covariance stretches the data our in the vertical and horizontal directions, while the full covariance stretches and rotates the data. In the next section, we will understand why.

A geometric interpretation of the covariance matrix

Recall from linear algebra that matrices are simply linear transformationsl thus, we can think of the covariance matrix as a linear transformation. In particular, we think of our data as white data (data with identity covariance) that was transformed by our covariance matrix. In other words, looking at our covariance matrix can tell us how our data was obtained. As we saw above, these transformations are stretches and rotations of our data; to see why and how it does this, we must first understand some important properties of the covariance matrix:

It turns out that $\Sigma$ is a symmetric positive semi-definite matrix. Let’s break this down:

1. Symmetric means that $\Sigma^T = \Sigma$. This makes sense, since all $\Sigma_{i,j} = \text{Cov}(X_i, X_j) = \text{Cov}(X_j, X_i) = \Sigma_{j,i}$
2. Positive semi-definite means that $x^T \Sigma x \geq 0$ for all $x \in \mathbb{R}^d$.

Why do these properties matter?

It can be shown that when a matrix is positive semi-definite, we can obtain its eigen-decomposition, where:

where $\Lambda$ is the eigenvalue matrix and $R$ is a rotation matrix, where the the columns of $R$ are eigenvectors. A slightly clearer way to express this is as $\Sigma = RSS^TR^{-1}$, where $S = \sqrt{\Lambda}$ and the values on the diagonal of $S$ tell you the amount by which each the data is stretched in the direction of each eigenvector. This might be confusing right now; hopefully the following examples will clear this up. The key idea for now is that we can now think of our data as white data that was transformed by a stretch and a rotation; to obtain the stretch and rotation we can use the eigendecomposition of the covariance matrix.

Seeing it in action

Here we will apply some transformations to some white data and then we will look at the covariance of the transformed data; if the statements above are true, we should be able to reverse-engineer the transformations from the covariance matrix.

Let’s start with a simple example. Let’s assume our white data was stretched by a factor of $4$ in the $x$-direction and $2$ in the $y$-direction; ie. it was transformed by $S = \text{diag}(4,2)$. Let’s see what this does to our data using some code:

white_data = np.random.multivariate_normal([0, 0], [[1, 0], [0, 1]], 1000)
x_w, y_w = white_data.T
S = np.array([[4, 0], [0, 2]])
S_X = T @ white_data.T
x_t, y_t = S_X
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))

ax1.plot(x_w, y_w, ".")
ax1.set_title("White data")
ax2.plot(x_t, y_t, ".")
ax2.set_title("Stretched data")


# Set aspect ratio and equal axis limits
ax1.set_aspect("equal")
ax2.set_aspect("equal")

lim = [-10, 10]

ax1.set_xlim(lim)
ax2.set_xlim(lim)
ax1.set_ylim(lim)
ax2.set_ylim(lim)


plt.tight_layout()
plt.show()

Now let’s compute the covariance matrix of our new data and round to the nearest integer:

V(S_X).round(0)

array([[16., -0.],
       [-0.,  4.]])

We get $\Sigma = \text{diag}(16, 4) = \text{diag}(4^2, 2^2) = \text{diag}(\sigma_x^2, \sigma_y^2)$. This is a diagonal matrix, so the eigenvalues can be read directly off the diagonal, and are 16 and 4 respectively, and the eigenvectors are the unit vectors. Using the formula above we have $\Sigma = RSS^TR^{-1} = I [\text{diag}(4,2)] [\text{diag}(4,2)]^T I$ (here the rotation matrix is the identity, since no rotation is applied). Indeed, this matches the claim from above, that states that the square roots of the eigenvalues are the amount by which the data is stretched in the directions of the eigenvectors.

What if we want to rotate it too? Let’s add a rotation matrix $R$ that rotates the data by $\theta$ radians, then our new transformation is a stretch and a rotation: $T = RS$. The formula for a rotation by $\theta$ radians in 2D is well known and has the form

We will use this in the code, where we will rotate by $\pi/4$ radians, then we will compute the eigenvectors and plot those too:

# Get the data
white_data = np.random.multivariate_normal([0, 0], [[1, 0], [0, 1]], 1000)
x_w, y_w = white_data.T
S = np.array([[4, 0], [0, 2]])
theta = np.pi / 4
R = np.array([[np.cos(theta), np.sin(theta)],[-np.sin(theta), np.cos(theta)]])
T_X = R @ S @ white_data.T
x_t, y_t = T_X
# Compute covariance and perform eigendecomposition
sigma = V(T_X.T).round(0)
eigenvalues, eigenvectors = np.linalg.eig(sigma)

# Plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))

ax1.plot(x_w, y_w, ".")
ax1.set_title("White data")
ax2.plot(x_t, y_t, ".")
ax2.set_title("Stretched and rotated data")


# Set aspect ratio and equal axis limits
ax1.set_aspect("equal")
ax2.set_aspect("equal")

# Display eigenvectors
for i in range(len(eigenvalues)):
    vec = eigenvectors[:, i]
    lam = eigenvalues[i]
    ax2.quiver(0, 0, vec[0]*np.sqrt(lam)*np.sign(lam), vec[1]*np.sqrt(lam)*np.sign(lam), angles='xy', scale_units='xy', scale=1,
              color='r', width=0.01, zorder=2)

lim = [-10, 10]

ax1.set_xlim(lim)
ax2.set_xlim(lim)
ax1.set_ylim(lim)
ax2.set_ylim(lim)


plt.tight_layout()
plt.show()

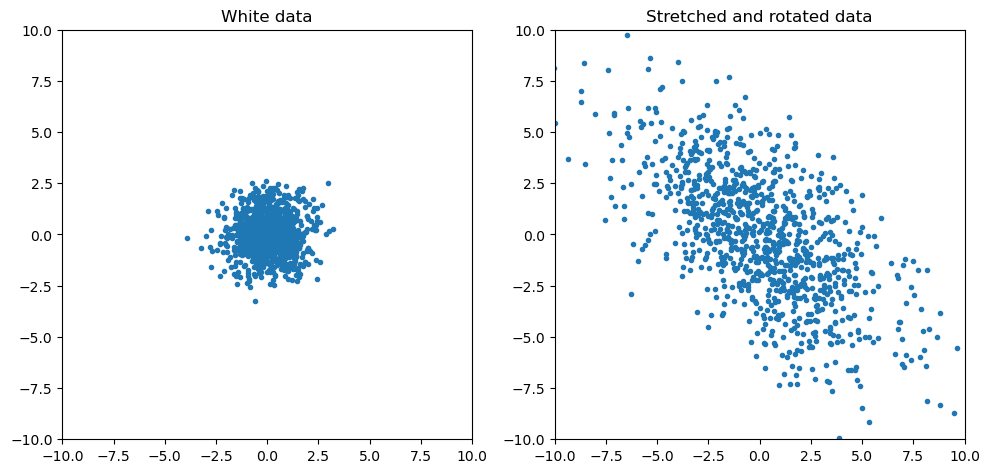
Again, if the statements from earlier hold, then we should be able to perform eigendecomposition on the covariance of our new data and obtain the matrices $S$ and $R$ we used to transform the data:

sigma = V(T_X.T).round(0)
eigenvalues, eigenvectors = np.linalg.eig(sigma)
np.allclose(eigenvectors, R) # True
np.allclose(np.sqrt(np.diag(eigenvalues)), S) # True

Thus, we see that indeed, the eigenvector matrix is the same as the rotation matrix, and the eigenvalues are the squares of the elements in the stretching matrix.

Conclusion

This blog post is pretty all over the place, but hopefully it provided a bit of clarification and insight into some ML topics that are often skimmed past in many books and courses.

References

• The Eigen-Decomposition: Eigenvalues and Eigenvectors
• Understanding Deep Learning by Simon J.D Prince
• Lesson 4: Multivariate Normal Distribution
• The Multivariate Gaussian Distribution
• Information about ellipses